松鼠小筑

1.进入官网找到自己所需的安装包：https://dev.mysql.com/  ，路径：DOWNLOAD-->MYSQL Community Edition(GRL)-->MYSQL on Windows (Installer & Tool)

或直接点击 https://dev.mysql.com/downloads/windows/installer/ 查看最新版本。

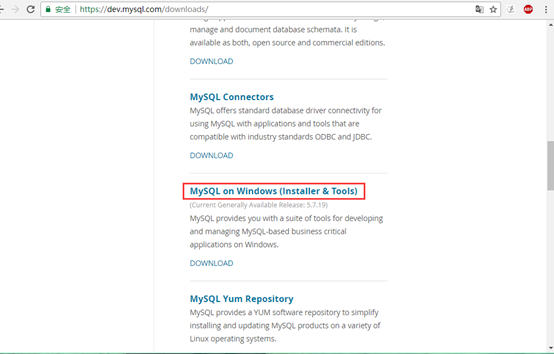
2.找到所需的安装包,

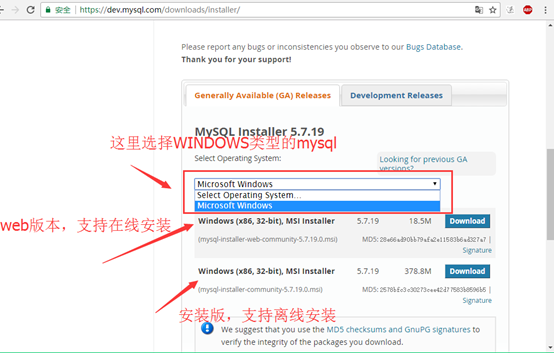
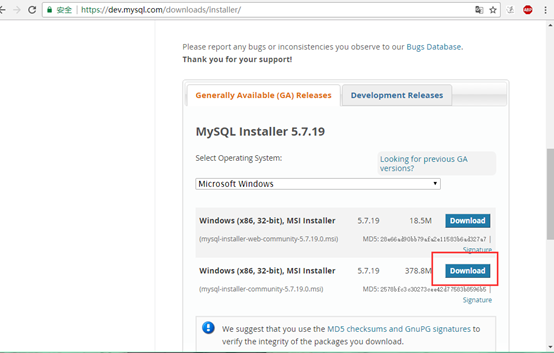
3.点击download。这里选择的是安装版（mysql -install-community）

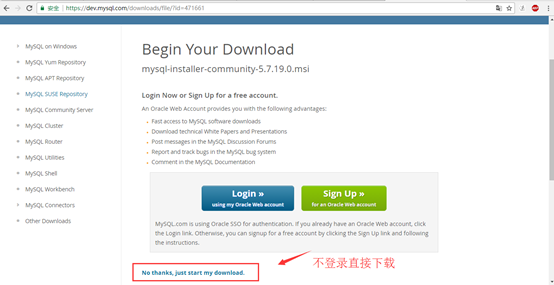
4.选择不登陆下载。

5.双击运行下载好的mysql-installer-community-5.7.19.0.msi，程序运行需要一些时间，请等待一下。

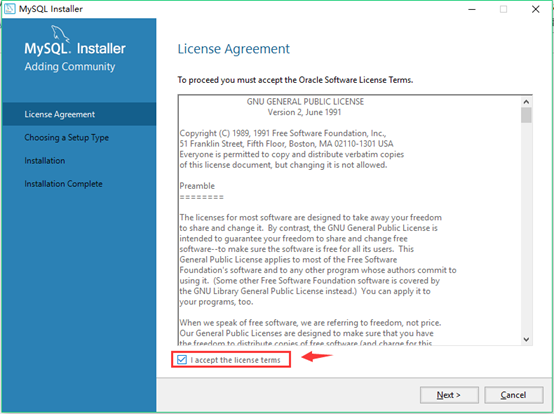
6.运行成功之后，进入欢迎的界面.选择我同意协议，不然无法进行下一步。

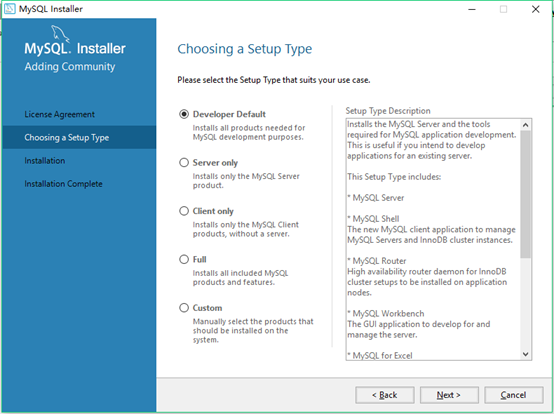
7. 进入类型选择页面，本人需要mysql云服务就选择了developer default（7.1是默认安装的步骤），如果只想安装mysql server的就选择custom模式（7.2步骤是选择自己需要的服务器类型，所选择的用于做一些数据分析）

• developer default（开发者默认）：安装mysql开发所需的所有产品
• server only（服务器）：只安装mysql服务器产品
• client only（客户端）：只安装没有服务器的mysql客户端产品
• full（完全）：安装所有包含的mysql产品和功能
• custom（手动）：手动选择系统上应安装的产品

7.1开发者默认模式检测以下程序会安装不成功，点击下一步进入下一个安装流程—>跳到第八步。

check requirements：以下产品的请求失败，安装程序将自动尝试解决其中一些问题。标记为手动的要求无法自动解决。单击这些项目以尝试手动恢复。

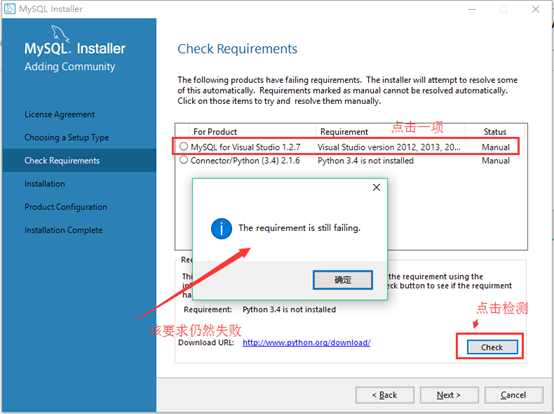
检测到不可安装的程序说明：

Visual Studio：是一款代码编辑工具（可编写C#、Visual Basic、C++、TypeScript、F# ），如果你安装的话就安装要求去安装Visual Studio version：2012.2013.2015.2017其中一个版本

Connector/pyton 3.4：电脑有python3.6了就没选择3.4版本的。如果你没安装有python可按要求去安装一些内容。

7.2选择mysql server（服务） 5.7.19 x64

选择mysql workbench(mysql 的工作薄) 6.3.9 x64

选择mysql notiyier(通知) 1.1.7 x86(因为这里只有一个选择所以选择了86)点击下一步进入下一个安装流程—>跳到第九步。

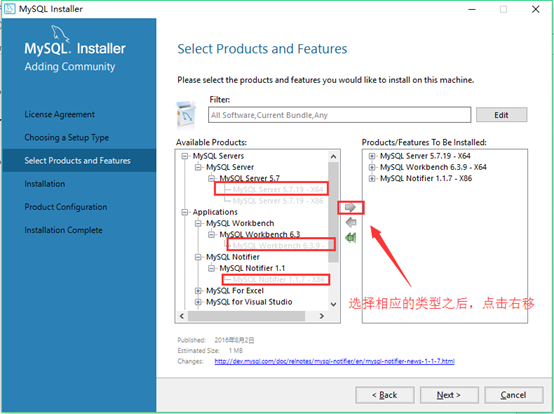
8.当我们点击下一步的时候安装程序出现了提示：（一个或者移动产品要求没有得到满足，那些符合要求的产品将不会安装/升级。你想要继续吗），这里我选择的是：YES

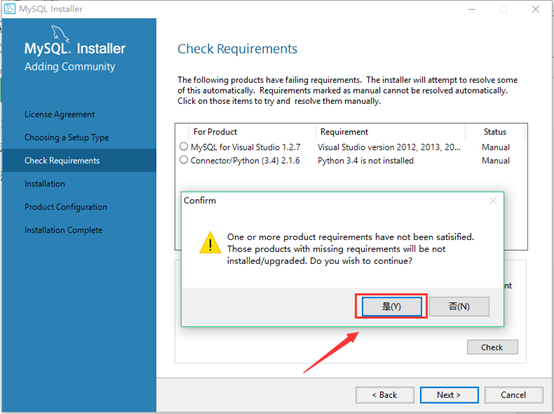
9.在安装所选界面能看到我们接下来所需要安装的程序，点击execute

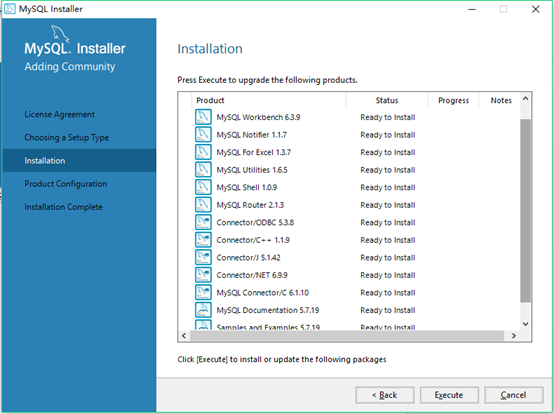
10安装程序进度界面，安装需要一些时间。点击dide tails能看到安装日志

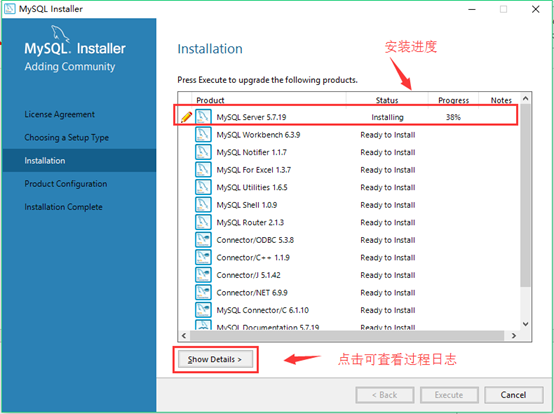
11.程序安装完成之后，点击next

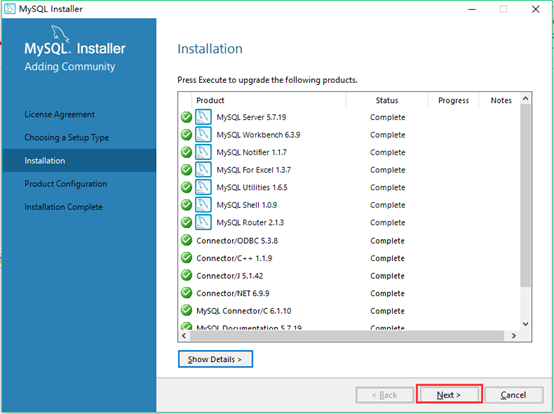
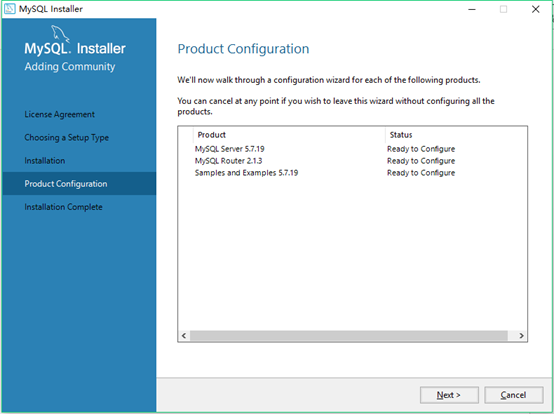
12.在product configutration（产品配置）页面能看到需要配置的程序，点击next（页面英语介绍：现在我们将逐一介绍以下产品的配置向导。您可以随时取消，如果您希望离开此向导，而不必配置所有产品）

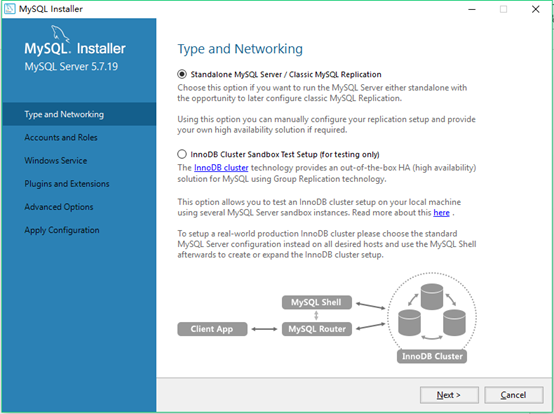
13.先配置mysql server的类型以及网络：type and networking（类型和网络），这里有两种mysql server类型，选择第一种类型点击next。

有两种类型简单介绍

• 1.standalone mysql server/classic mysql replication：独立的mysql服务器/经典的mysql复制。choose this option if you want to run the mysql server either standalone with the opportunity to later configure classic mysql replication：选择这个选项，如果你想运行mysql服务器是独立的，有机会以后配置经典的mysql复制
• 2. innodb cluster sandbox thst setup(for testing only)：

innodb集群沙箱thst设置（仅用于测试）

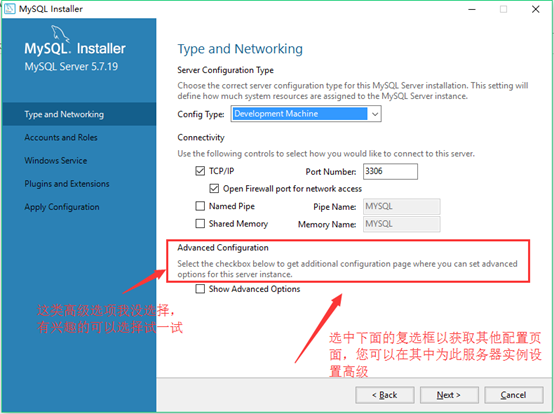
14.设置服务器配置类型以及连接端口：继续next

Config Type:选择Development Machine，用于小型以及学习所用足够了。

Port number：输入3306，也可以输入其他最好是3306-3309之间。

15.配置root的密码（该密码要记住），系统提示这密码虚弱

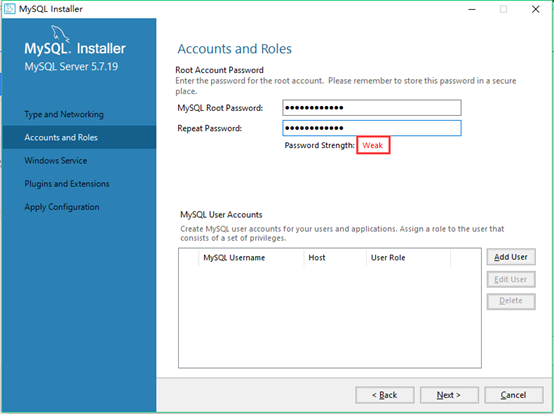
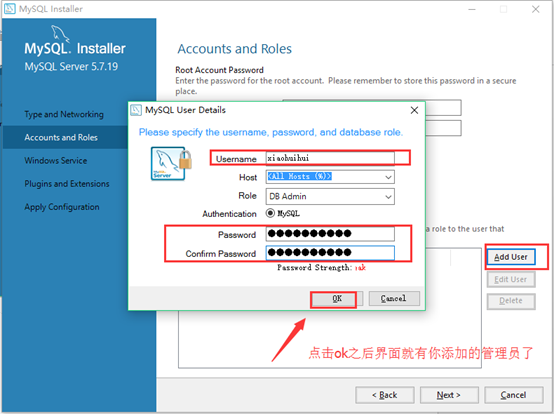
16. 添加其他管理员，点击add user 输入账号密码点击ok（如果添加的管理员只允许在本地登录就将host改成local），回到界面之后点击next

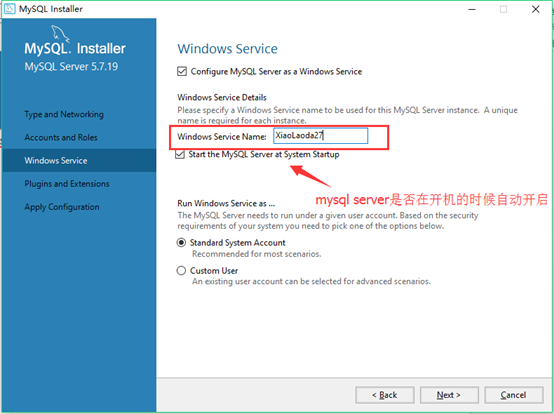
17.配置mysql在windows系统中的名字，是否选择开机启动mysql服务，其它的没进行修改，点击"Next"。

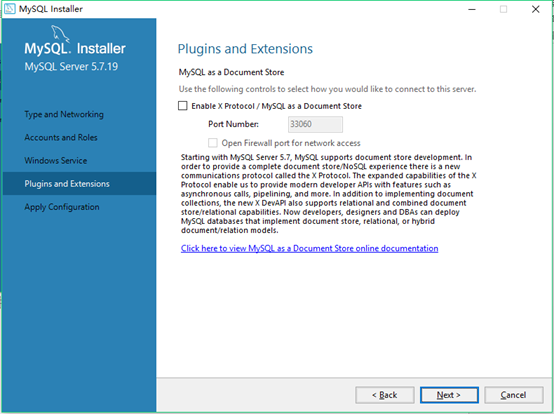
18.配置插件和扩展页面没进行修改直接下一步：

19.Mysql server :apply configuration（应用配置页面），选择execute进行安装配置

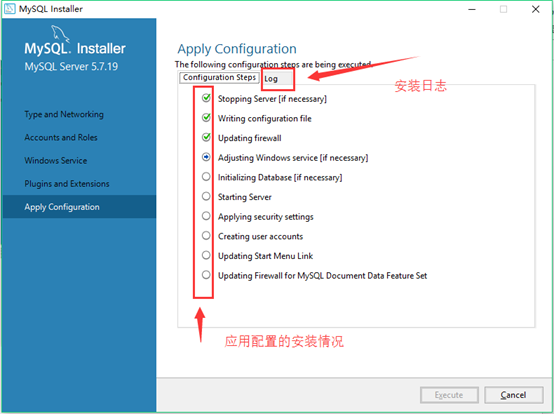
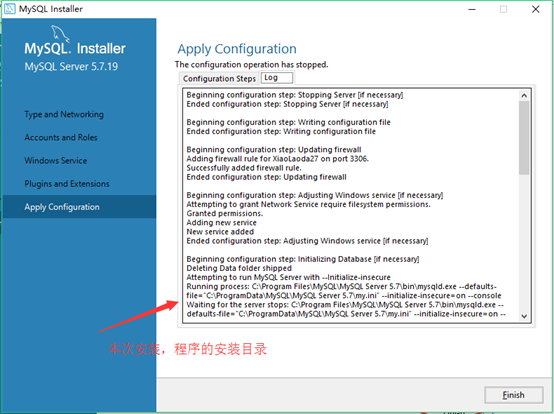
20. mysql server应用配置的log，选择finish

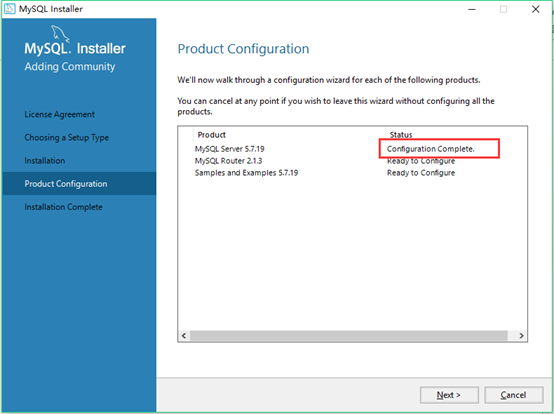
21.安装程序又回到了product configutration（产品配置）页面，此时我们看到mysql server安装成功的显示，继续下一步：

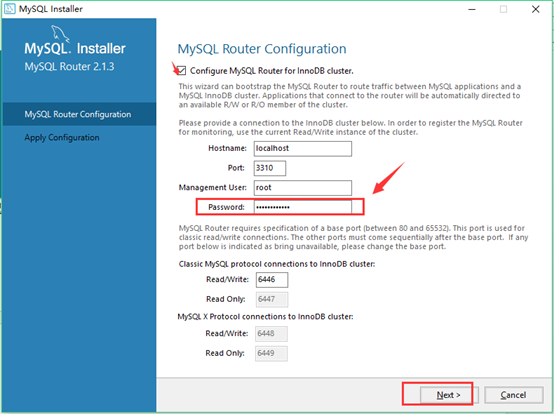
22. 配置mysql router：勾选configure mysql route for innoDB cluster之后输入密码。（如果不想输入密码可直接点击点一下）点击下一步

23.Mysql router :apply configuration（应用配置页面）点击execute,

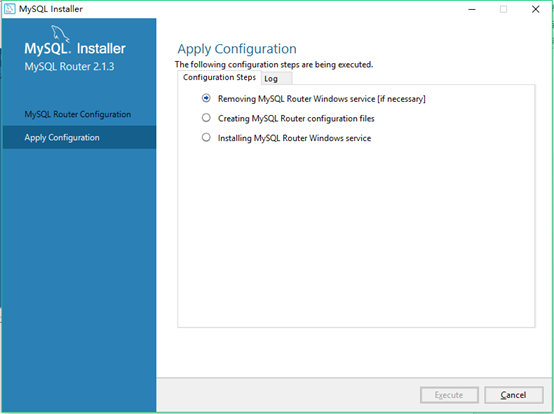
24.安装完成之后点击选择finish

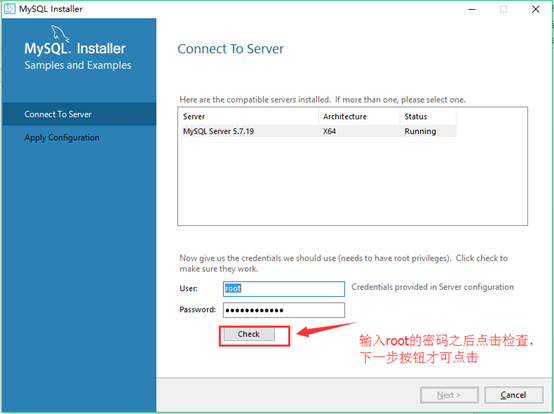
25.检测root密码

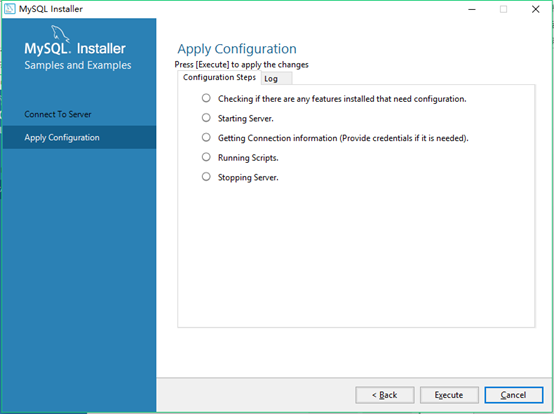
26.安装一些server，老规矩点击execute，完成之后点击finish

27. 程序回到产品配置页面。继续下一步：

28.安装程序完成界面。

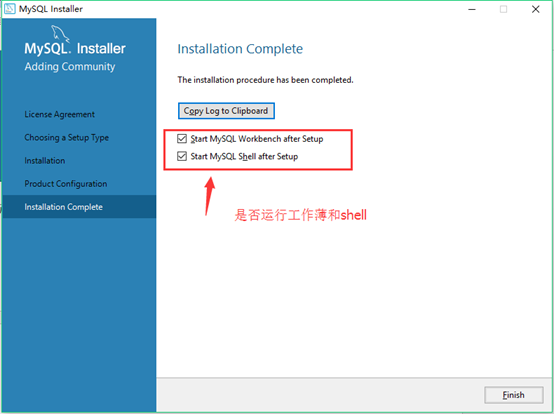
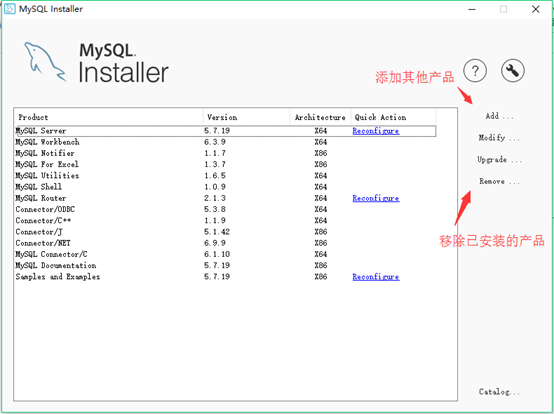
29. 双击运行之前下载的安装包，能看到我们所安装的产品。

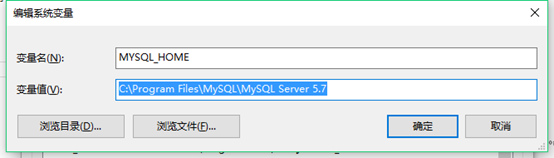
30. 配置mysql环境变量

上面安装的是时候我们看到mysql默认安装路径是：C:\Program Files\MySQL\MySQL Server 5.7

我的电脑右键—>属性à高级系统设置à环境变量à新建MYSQL_HOME,将安装目录输入：

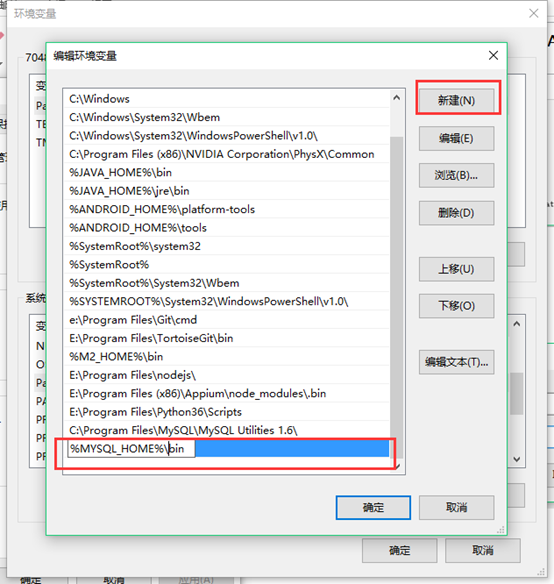
找到path编辑：输入%MYSQL_HOME%\bin

打开cmd输入mysql –u root –p

输入root的密码

首先，排序算法的稳定性大家应该都知道，通俗地讲就是能保证排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。在简单形式化一下，如果Ai = Aj，Ai原来在位置前，排序后Ai还是要在Aj位置前。

      其次，说一下稳定性的好处。排序算法如果是稳定的，那么从一个键上排序，然后再从另一个键上排序，第一个键排序的结果可以为第二个键排序所用。基数排序就是这样，先按低位排序，逐次按高位排序，低位相同的元素其顺序再高位也相同时是不会改变的。另外，如果排序算法稳定，对基于比较的排序算法而言，元素交换的次数可能会少一些（个人感觉，没有证实）。

回到主题，现在分析一下常见的排序算法的稳定性，每个都给出简单的理由。

(1)冒泡排序

冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较，交换也发生在这两个元素之间。所以，如果两个元素相等，我想你是不会再无聊地把他们俩交换一下的；如果两个相等的元素没有相邻，那么即使通过前面的两两交换把两个相邻起来，这时候也不会交换，所以相同元素的前后顺序并没有改变，所以冒泡排序是一种稳定排序算法。

(2)选择排序

选择排序是给每个位置选择当前元素最小的，比如给第一个位置选择最小的，在剩余元素里面给第二个元素选择第二小的，依次类推，直到第n - 1个元素，第n个元素不用选择了，因为只剩下它一个最大的元素了。那么，在一趟选择，如果当前元素比一个元素小，而该小的元素又出现在一个和当前元素相等的元素后面，那么交换后稳定性就被破坏了。比较拗口，举个例子，序列5 8 5 2 9，我们知道第一遍选择第1个元素5会和2交换，那么原序列中2个5的相对前后顺序就被破坏了，所以选择排序不是一个稳定的排序算法。

(3)插入排序
插入排序是在一个已经有序的小序列的基础上，一次插入一个元素。当然，刚开始这个有序的小序列只有1个元素，就是第一个元素。比较是从有序序列的末尾开始，也就是想要插入的元素和已经有序的最大者开始比起，如果比它大则直接插入在其后面，否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面。所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳定的。

(4)快速排序
快速排序有两个方向，左边的i下标一直往右走，当a[i] <= a[center_index]，其中center_index是中枢元素的数组下标，一般取为数组第0个元素。而右边的j下标一直往左走，当a[j] > a[center_index]。如果i和j都走不动了，i <= j，交换a[i]和a[j],重复上面的过程，直到i > j。 交换a[j]和a[center_index]，完成一趟快速排序。在中枢元素和a[j]交换的时候，很有可能把前面的元素的稳定性打乱，比如序列为5 3 3 4 3 8 9 10 11，现在中枢元素5和3（第5个元素，下标从1开始计）交换就会把元素3的稳定性打乱，所以快速排序是一个不稳定的排序算法，不稳定发生在中枢元素和a[j] 交换的时刻。

(5)归并排序
归并排序是把序列递归地分成短序列，递归出口是短序列只有1个元素（认为直接有序）或者2个序列（1次比较和交换），然后把各个有序的段序列合并成一个有序的长序列，不断合并直到原序列全部排好序。可以发现，在1个或2个元素时，1个元素不会交换，2个元素如果大小相等也没有人故意交换，这不会破坏稳定性。那么，在短的有序序列合并的过程中，稳定是是否受到破坏？没有，合并过程中我们可以保证如果两个当前元素相等时，我们把处在前面的序列的元素保存在结果序列的前面，这样就保证了稳定性。所以，归并排序也是稳定的排序算法。

(6)基数排序
基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序，最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。基数排序基于分别排序，分别收集，所以其是稳定的排序算法。

(7)希尔排序(shell)
希尔排序是按照不同步长对元素进行插入排序，当刚开始元素很无序的时候，步长最大，所以插入排序的元素个数很少，速度很快；当元素基本有序了，步长很小， 插入排序对于有序的序列效率很高。所以，希尔排序的时间复杂度会比O(n^2)好一些。由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以shell排序是不稳定的。

(8)堆排序
我们知道堆的结构是节点i的孩子为2 * i和2 * i + 1节点，大顶堆要求父节点大于等于其2个子节点，小顶堆要求父节点小于等于其2个子节点。在一个长为n 的序列，堆排序的过程是从第n / 2开始和其子节点共3个值选择最大（大顶堆）或者最小（小顶堆），这3个元素之间的选择当然不会破坏稳定性。但当为n / 2 - 1， n / 2 - 2， ... 1这些个父节点选择元素时，就会破坏稳定性。有可能第n / 2个父节点交换把后面一个元素交换过去了，而第n / 2 - 1个父节点把后面一个相同的元素没 有交换，那么这2个相同的元素之间的稳定性就被破坏了。所以，堆排序不是稳定的排序算法。

综上，得出结论: 选择排序、快速排序、希尔排序、堆排序不是稳定的排序算法，而冒泡排序、插入排序、归并排序和基数排序是稳定的排序算法

长度为n的折半查找判定树的构造方法为：

⑴ 当n=0时，折半查找判定树为空；

⑵ 当n＞0时，折半查找判定树的根结点是有序表中序号为mid=(n+1)/2的记录，根结点的左子树是与有序表r[1] ~ r[mid-1]相对应的折半查找判定树，根结点的右子树是与r[mid+1] ~ r[n]相对应的折半查找判定树。

例如，长度为10的折半查找判定树的具体生成过程为：

⑴ 在长度为10的有序表中进行折半查找，不论查找哪个记录，都必须先和中间记录进行比较，而中间记录的序号为(1+10)/2=5（注意是整除即向下取整），即判定树的根结点是5，如图7-2(a)所示；

⑵ 考虑判定树的左子树，即将查找区间调整到左半区，此时的查找区间是

[1，4]，也就是说，左分支上为根结点的值减1，代表查找区间的高端high，此时，根结点的左孩子是(1+4)/2=2，如图7-2(b)所示；

⑶ 考虑判定树的右子树，即将查找区间调整到右半区，此时的查找区间是

[6，10]，也就是说，右分支上为根结点的值加1，代表查找区间的低端low，此时，根结点的右孩子是(6+10)/2=8，如图7-2(c)所示；

⑷ 重复⑵⑶步，依次确定每个结点的左右孩子，如图7-2(d)所示。

对于折半查找判定树，需要补充以下两点： 
⑴ 折半查找判定树是一棵二叉排序树，即每个结点的值均大于其左子树上所有结点的值，小于其右子树上所有结点的值； 
⑵ 折半查找判定树中的结点都是查找成功的情况，将每个结点的空指针指向一个实际上并不存在的结点——称为外结点，所有外结点即是查找不成功的情况，如图7-2(e)所示。如果有序表的长度为n，则外结点一定有n+1个。 在折半查找判定树中，某结点所在的层数即是查找该结点的比较次数，整个判定树代表的有序表的平均查找长度即为查找每个结点的比较次数之和除以有序表的长度。例如，长度为10的有序表的平均查找长度为： 
ASL=(1×1+2×2+3×4+4×3)/10=29/10 
在折半查找判定树中，查找不成功时的比较次数即是查找相应外结点时与内结点的比较次数。整个判定树代表的有序表在查找失败时的平均查找长度即为查找每个外结点的比较次数之和除以外结点的个数。例如，长度为10的有序表在查找失败时的平均查找长度为： 
ASL=(3×5+4×6)/11=39/11

以二叉链表作为二叉树的存储结构，求二叉树的叶子结点个数。

输入格式:

输入二叉树的先序序列。

提示：一棵二叉树的先序序列是一个字符串，若字符是‘#’,表示该二叉树是空树，否则该字符是相应结点的数据元素。

输出格式:

输出有两行：

第一行是二叉树的中序遍历序列；

第二行是二叉树的叶子结点个数。

输入样例:

ABC##DE#G##F###

输出样例:

CBEGDFA

3

需要三个函数：前序建立树，中序输出，计算叶子结点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

//根据有#的前序遍历生成树
tree fcreate()
{
    tree t;
    char s;
    //按每个字符输入
    scanf("%c",&s);
    if(s=='#')return nullptr;
    else {
        t=(tree)malloc(sizeof(struct treenode));
        t->data = s;
        t->lchild = fcreate();
        t->rchild = fcreate();
        return t;
    }
}

//中序输出
void Inordertranverse(tree t)
{
    if(!t)return;
    Inordertranverse(t->lchild);
    cout<<t->data;
    Inordertranverse(t->rchild);
}

//计数树的根结点数
int count(tree t,int c)
{
    if(t) {
        if (t->lchild == nullptr && t->rchild == nullptr)c++;
        c=count(t->lchild, c);
        c=count(t->rchild, c);
    }
    return c;
}

以二叉链表作为二叉树的存储结构，交换二叉树中每个结点的左孩子和右孩子。

输入格式:

输入二叉树的先序序列。

提示：一棵二叉树的先序序列是一个字符串，若字符是‘#’,表示该二叉树是空树，否则该字符是相应结点的数据元素。

输出格式:

输出有两行：

第一行是原二叉树的中序遍历序列；

第二行是交换后的二叉树的中序遍历序列。

输入样例:

ABC##DE#G##F###

输出样例:

CBEGDFA

AFDGEBC

需要三个函数：根据前序输入生成树，交换，中序输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

//根据有#的前序遍历生成树
tree fcreate()
{
    tree t;
    char s;
    //按每个字符输入
    scanf("%c",&s);
    if(s=='#')return nullptr;
    else {
        t=(tree)malloc(sizeof(struct treenode));
        t->data = s;
        t->lchild = fcreate();
        t->rchild = fcreate();
        return t;
    }
}
void Inordertranverse(tree t)
{
    if(!t)return;
    Inordertranverse(t->lchild);
    cout<<t->data;
    Inordertranverse(t->rchild);
}

//交换每个结点左右子树
void Exchange(tree &bt)
{
    tree temp;
    if(bt){
        temp = bt -> lchild;
        bt -> lchild = bt -> rchild;
        bt -> rchild = temp;
        Exchange(bt -> lchild);
        Exchange(bt -> rchild);
    }
}
int main()
{
    tree t;
    t=fcreate();
    Inordertranverse(t);
    Exchange(t);
    Inordertranverse(t);
}