Deep-Learning
Learning note for the course Deep Learning Specialization
Neural Networks and Deep Learning
Introduction to Deep Learning
Neural network:
有一个输入x,经过一些神经元后计算得到结果y。所以线性回归是一个神经元的神经网络。
复杂模型如预测房价的时候可以有多个神经元
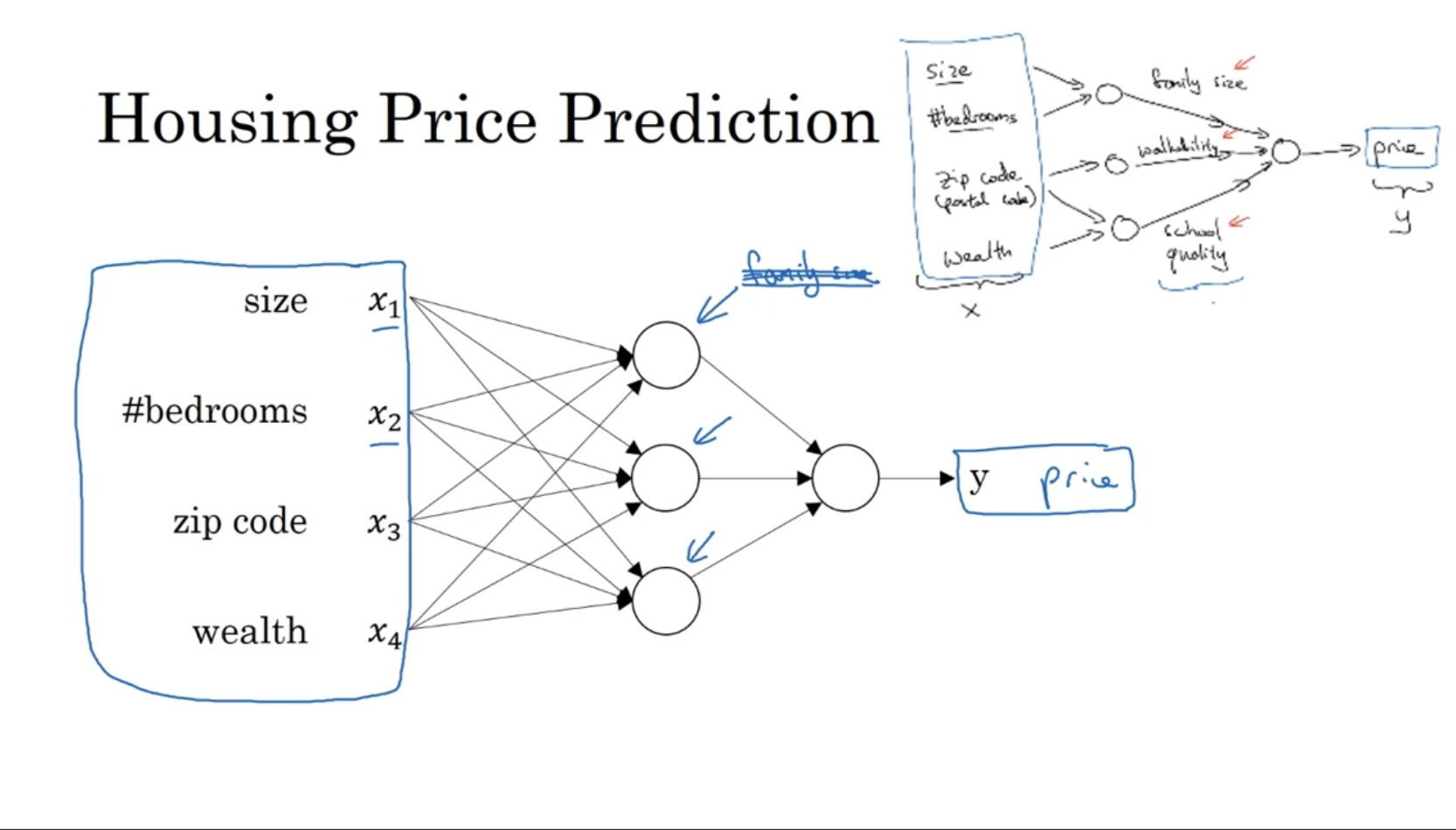
Structured Data:如存在数据库里的数据
Unstructured Data: 如图片,音频,视频
要想提升预测的准确性,要不就使用更多数据,要不就使用更大的神经网络模型。
Notations
General comments:
- superscript \((i)\) will denote the \(i^{\text{th}}\) training example while superscript \([l]\) will denote the \(l^{\text{th}}\) layer
Sizes:
\(m\): number of examples in the dataset
\(n_x\): input size
\(n_y\): output size (or number of classes)
\(n_h^{[l]}\): number of hidden units of the \(l^{\text{th}}\) layer
In a for loop, it is possible to denote \(n_x = n_h^{[0]}\) and \(n_y = n_h^{[\text{number of layers} + 1]}\).
\(L\): number of layers in the network.
Objects:
- \(X \in \mathbb{R}^{n_x \times m}\) is the input matrix
- \(x^{(i)} \in \mathbb{R}^{n_x}\) is the \(i^{\text{th}}\) example represented as a column vector
- \(Y \in \mathbb{R}^{n_y \times m}\) is the label matrix
- \(y^{(i)} \in \mathbb{R}^{n_y}\) is the output label for the \(i^{\text{th}}\) example
- \(W^{[l]} \in \mathbb{R}^{\text{number of units in next layer} \times \text{number of units in the previous layer}}\) is the weight matrix, superscript \([l]\) indicates the layer
- \(b^{[l]} \in \mathbb{R}^{\text{number of units in next layer}}\) is the bias vector in the \(l^{\text{th}}\) layer
- \(\hat{y} \in \mathbb{R}^{n_y}\) is the predicted output vector. It can also be denoted \(a^{[L]}\) where \(L\) is the number of layers in the network.
Common forward propagation equation examples:
- \(a = g^{[l]}(W^{[l]}x^{(i)} + b_1) = g^{[l]}(z_1)\) where \(g^{[l]}\) denotes the \(l^{\text{th}}\) layer activation function
- \(\hat{y}^{(i)} = \text{softmax}(W_{hh} + b_2)\)
General Activation Formula:
\(a_j^{[l]} = g^{[l]}\left(\sum_k w_{jk}^{[l]} a_k^{[l-1]} + b_j^{[l]}\right) = g^{[l]}(z_j^{[l]})\)
\(J(x, W, b, y)\) or \(J(\hat{y}, y)\) denote the cost function.
Examples of cost function:
- \(J_{\text{CE}}(\hat{y}, y) = -\sum_{i=0}^m y^{(i)} \log \hat{y}^{(i)}\)
- \(J_1(\hat{y}, y) = \sum_{i=0}^m | y^{(i)} - \hat{y}^{(i)} |\)
Logistic Regression as a Neural Network
Defination
例:给一个二元分类问题:分辨图片里是不是猫
输入是一个\(n_x\)维数组,即图片的像素值。输出\(\hat y\) 即y的预测值。\(z = w^Tx + b\)
对于二分问题, 输出\(\hat{y} = w^Tx + b\),但是他会返回超出0-1范围的值,这时我们就需要加一个sigmoid函数来约束输出结果的范围,这就是逻辑回归。
\(\hat{y} = \sigma(w^Tx + b)\)
\(\sigma(z) = 1/(1+e^{-z})\)
Cost function
然后需要找到w和b的值,w是一个nx维数组,b是一个值。
损失函数\(l(\hat y,y)\)接收预测值和真实值,在逻辑回归中使用下边这个损失函数。
\(L(\hat y,y) = -(y\log \hat y + (1-y)\log (1-\hat y))\)
Loss function computes the error for a single training example; the cost function is the average of the loss functions of the entire training set.
有了loss function后就可以定义cost function \(J(w,b) = \frac{1}{m}\sum_{i=1}^m L(\hat y^{(i)},y^{(i)})\)
用这个函数可以获得最优的w和b。
Gradient Descent
有了cost function后需要找到可以把它最小化的w和b参数。这里我们可以使用梯度下降法。
我们使用的cost function是convex的,所以只有一个全局最小值。
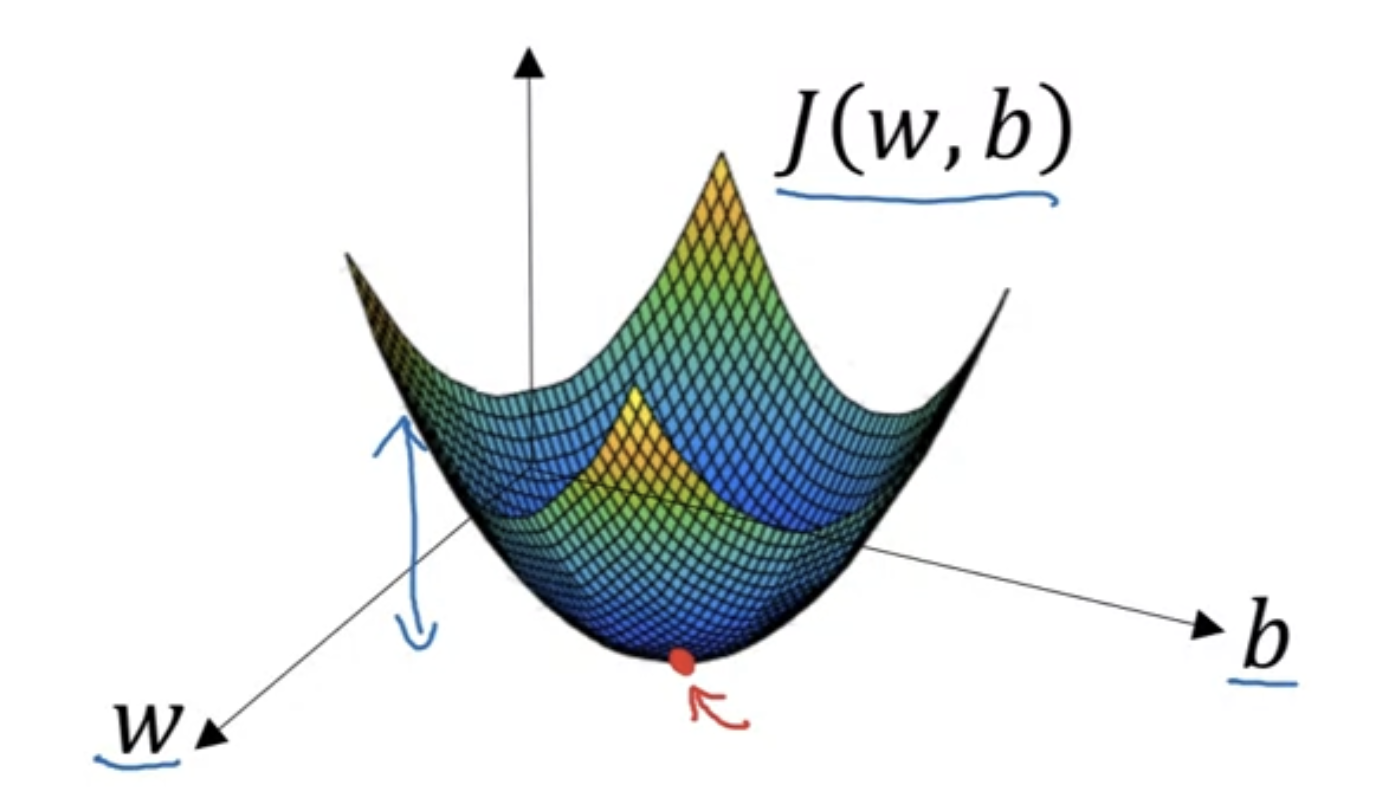
具体做法:定义一个learning rate \(\alpha\) ,然后重复计算。
Cost Function:
\(J(\omega, b)\)
Gradient Descent Updates:
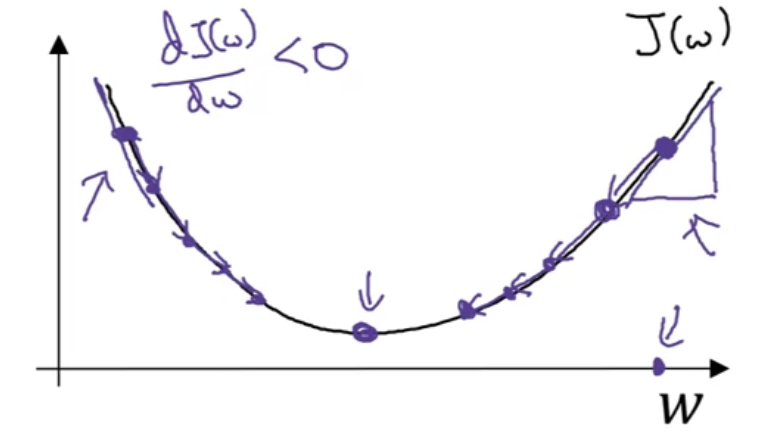
\(\omega := \omega - \alpha \frac{\partial J(\omega, b)}{\partial \omega}\)
\(b := b - \alpha \frac{\partial J(\omega, b)}{\partial b}\)
这里\(\frac{dJ(w)}{dw}\)是J在x=w点处的斜率,即导数。有两个变量的时候就算偏导数。
对于单个输入的情况我们有
\(z = w^T x + b\)
\(\hat{y} = a = \sigma(z)\)
\(\mathcal{L}(a, y) = -(y \log(a) + (1 - y) \log(1 - a))\)
\(\sigma(z) = 1/(1+e^{-z})\)
在得到L后现在要反向计算w和b的值
假设输入有两个特征x1和x2,那么有下图:
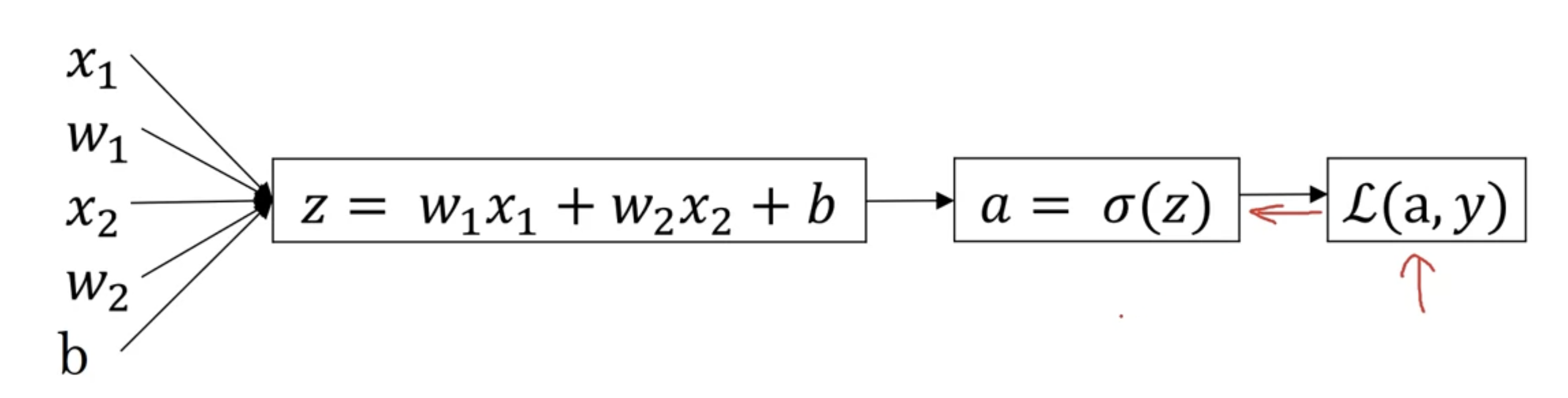
然后计算导数da,给L求a的偏导得到\(\frac{dL(a,y)}{da} = -\frac{y}{a} + \frac{1-y}{1-a}\)
然后计算\(dz = \frac{dL}{da}*\frac{da}{dz} = a-y\)
这里\(\frac{da}{dz}\)是sigmoid函数的导数,计算方法如下:
The sigmoid function is defined as:
\[ \sigma(x) = \frac{1}{1 + e^{-x}} \]
To find the derivative of ((x)) with respect to (x), we apply the chain rule. Let:
\[ y = \sigma(x) = \frac{1}{1 + e^{-x}} \]
Now, differentiate (y) with respect to (x):
\[ \frac{dy}{dx} = \frac{d}{dx} \left( (1 + e^{-x})^{-1} \right) \]
Using the chain rule, where ( u = 1 + e^{-x} ) and ( y = u^{-1} ), we get:
\[ \frac{dy}{dx} = -1 \cdot u^{-2} \cdot \frac{du}{dx} \]
Now, differentiate ( u ) with respect to (x):
\[ \frac{du}{dx} = \frac{d}{dx} (1 + e^{-x}) = 0 + (-e^{-x}) = -e^{-x} \]
Substitute () back into the derivative:
\[ \frac{dy}{dx} = - \frac{1}{(1 + e^{-x})^2} \cdot (-e^{-x}) \]
This simplifies to:
\[ \frac{dy}{dx} = \frac{e^{-x}}{(1 + e^{-x})^2} \]
Notice that ( (x) = ), so:
\[ \frac{dy}{dx} = \frac{e^{-x}}{1 + e^{-x}} \cdot \frac{1}{1 + e^{-x}} = \sigma(x) \cdot \left(1 - \sigma(x)\right) \]
Therefore, the derivative of the sigmoid function is:
\[ \frac{d\sigma(x)}{dx} = \sigma(x) \cdot (1 - \sigma(x)) \]
在计算的时候可以使用for loop实现,但是计算起来效率很低,因此可以使用向量化来计算。
Vectorization
如果想计算for i in range t: z += w[i] * x[i] + b[i]的话可以使用np.dot函数来代替。
Shallow Neural Networks
神经网络中中括号的上标[1] [2]代表神经网络的层数,第几层。
Neural Network Representation
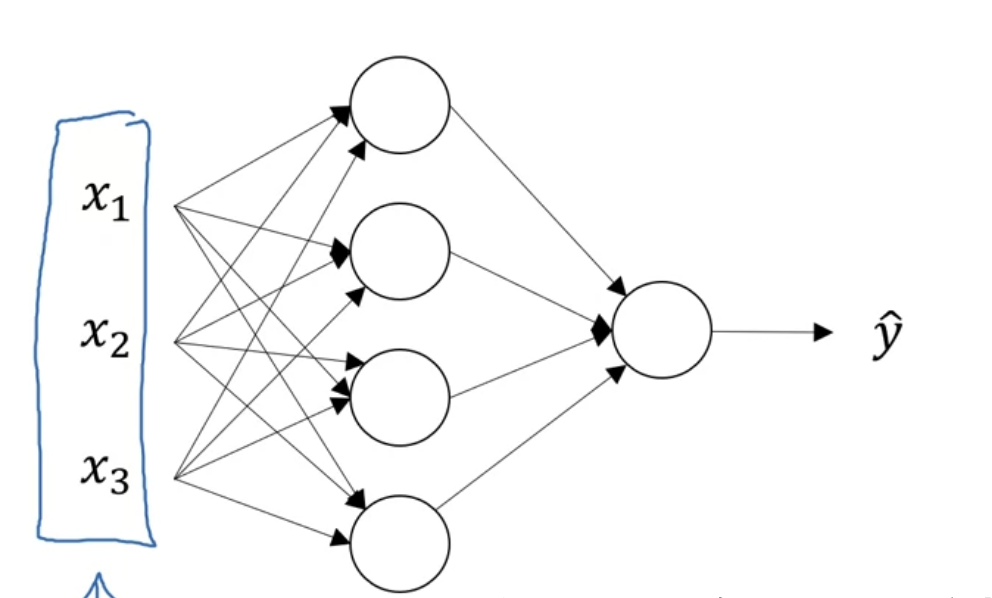
最左边一列是输入层input layer
第二列是隐藏层hidden layer,这层里的数据是看不到的
第三列是输出层output layer
我们可以用\(a^{[0]}=x\)代表第一层,那么\(\hat {y} = a^{[2]}\)
The number of rows in W[k] is the number of neurons in the k-th layer and the number of columns is the number of inputs of the layer.
The number of columns in Z[1] and A[1] is equal to the number of examples in the batch, m. And the number of rows inZ*[1] and A[1] is equal to the number of neurons in the first layer.
针对单一案例的神经网络训练
假设现在有一个神经网络,第一层有四个node,每一个节点中都进行一次逻辑回归,在多层网络中计算方式为: \[ z_1^{[1]} = w_1^{[1]T} x + b_1^{[1]}, \quad a_1^{[1]} = \sigma(z_1^{[1]}) \]
\[ z_2^{[1]} = w_2^{[1]T} x + b_2^{[1]}, \quad a_2^{[1]} = \sigma(z_2^{[1]}) \]
这里第一层的第一个node用自己的w和b,然后结果再用sigmoid处理得到结果a。
在向量化计算的时候,首先W矩阵是一个4,3的矩阵。每一行都是三个针对每一个特征x的不一样的w值,代表这个node的w值,有四行代表第一层的四个node。这里x有1,2,3是因为这个特征需要用三个值来表示,例如点的坐标xyz值。这里x数量也可以有很多,如在图像中就可能对于每一个输入都有64个x,就需要在每个node里有64个w,这时X就是(64,1),W就是(4,64)如果第一层有4个结点。
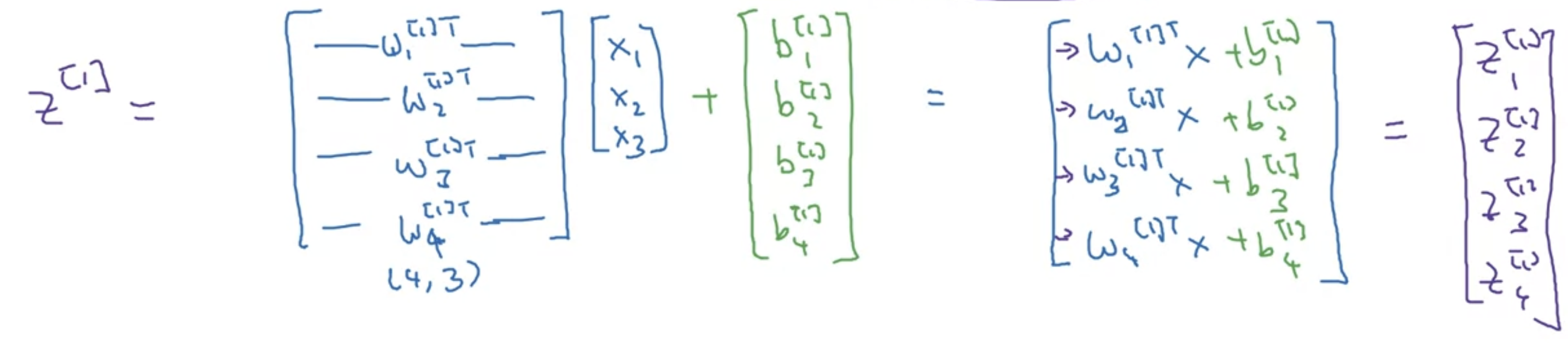
这里乘法全都是矩阵点乘。
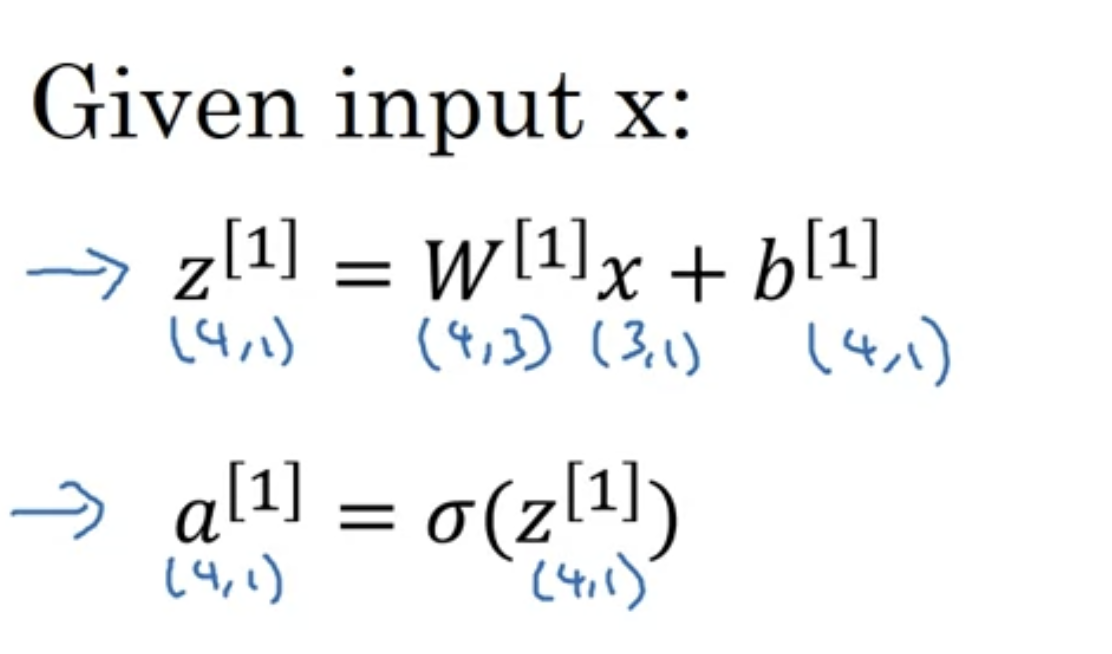
这里x也可以写成\(A^0\),下一步就是用A1矩阵计算。
针对多个输入的神经网络
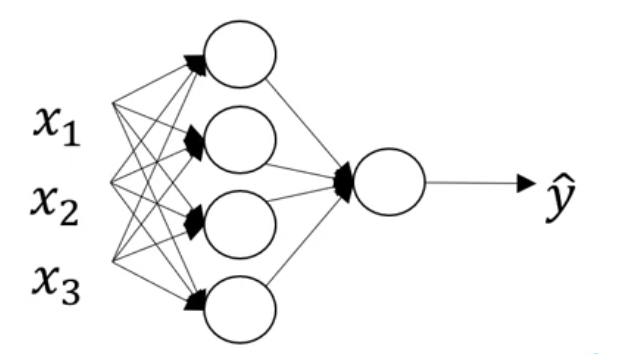
正向传播的时候流程如下: for (i = 1) to (m):
\[ z^{[1]}(i) = W^{[1]} x(i) + b^{[1]} \]
\[ a^{[1]}(i) = \sigma(z^{[1]}(i)) \]
\[ z^{[2]}(i) = W^{[2]} a^{[1]}(i) + b^{[2]} \]
\[ a^{[2]}(i) = \sigma(z^{[2]}(i)) \]
对于每个x都计算一下。
在矢量化实现的时候,首先需要有一个X矩阵,他是所有x按列堆叠产物。结果也是Z和a按列堆叠得到的。
Activation functions
Sigmoid:\(\sigma(z) = 1/(1+e^{-z})\)
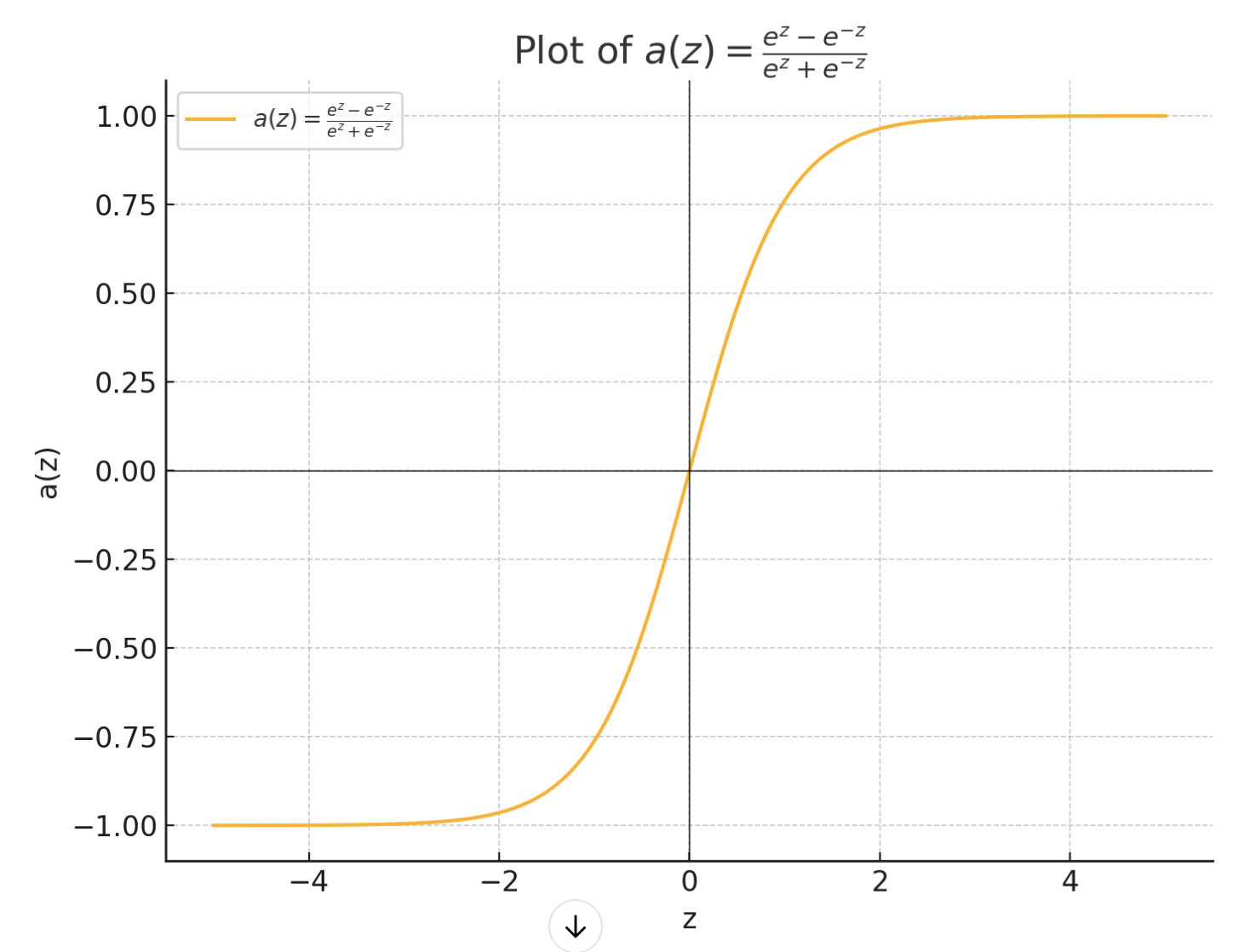
Tanh: \(a = \frac{e^z - e^{-z}}{e^z+e^{-z}}\)
ReLU: a = max(0,z)
在隐藏层使用tanhx或relu,在输出层使用sigmoid,因为我们想要输出范围是0-1.
神经网络的反向传播
反向传播的时候首先需要计算激活函数的导数:
sigmoid:
\(g(z) = 1/(1+e^{-z})\)
g'(z) = g(z)(1-g(z))
Tanh:
\(g(z) = \frac{e^z - e^{-z}}{e^z+e^{-z}}\)
\(g'(z) = 1 - g(z)^2\)
ReLU: g(z) = max(0,z)
g'(z) = 0/1
然后需要使用Gradient descent
假设只有一层隐藏层,有如下参数:\(w^{[1]}\)\(b^{[1]}\)\(w^{[2]}\)\(b^{[2]}\)
输入有\(n_x\)个特征,\(n_1\)个隐藏单元和\(n_2\)个输出单元。
我们有如下cost function:\(J((w^{[1]},b^{[1]},w^{[2]},b^{[2]})) = 1/m \sum^m_{i=1}L(\hat y,y)\)
这里\(\hat y\)是输出的预测,也就是\(a^[2]\).
计算梯度下降
首先随机获取参数w和b
重复:
- 计算从i到m的对于参数的预测值\(\hat y\)
- 计算dw1,db1,dw2,db2
- 更新参数,w1 = w1 - \(\alpha dw^1\), b1 = b1 - \(\alpha db^1\)
直到到达预设的迭代次数。
代码部署
案例:给一系列点坐标,做二分分类
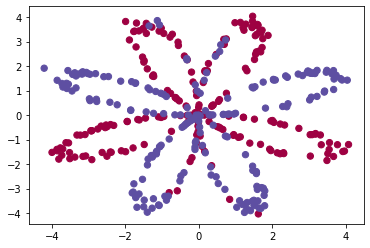
实现一个如下图所示的模型:两个输入是因为每个点有x,y两个值
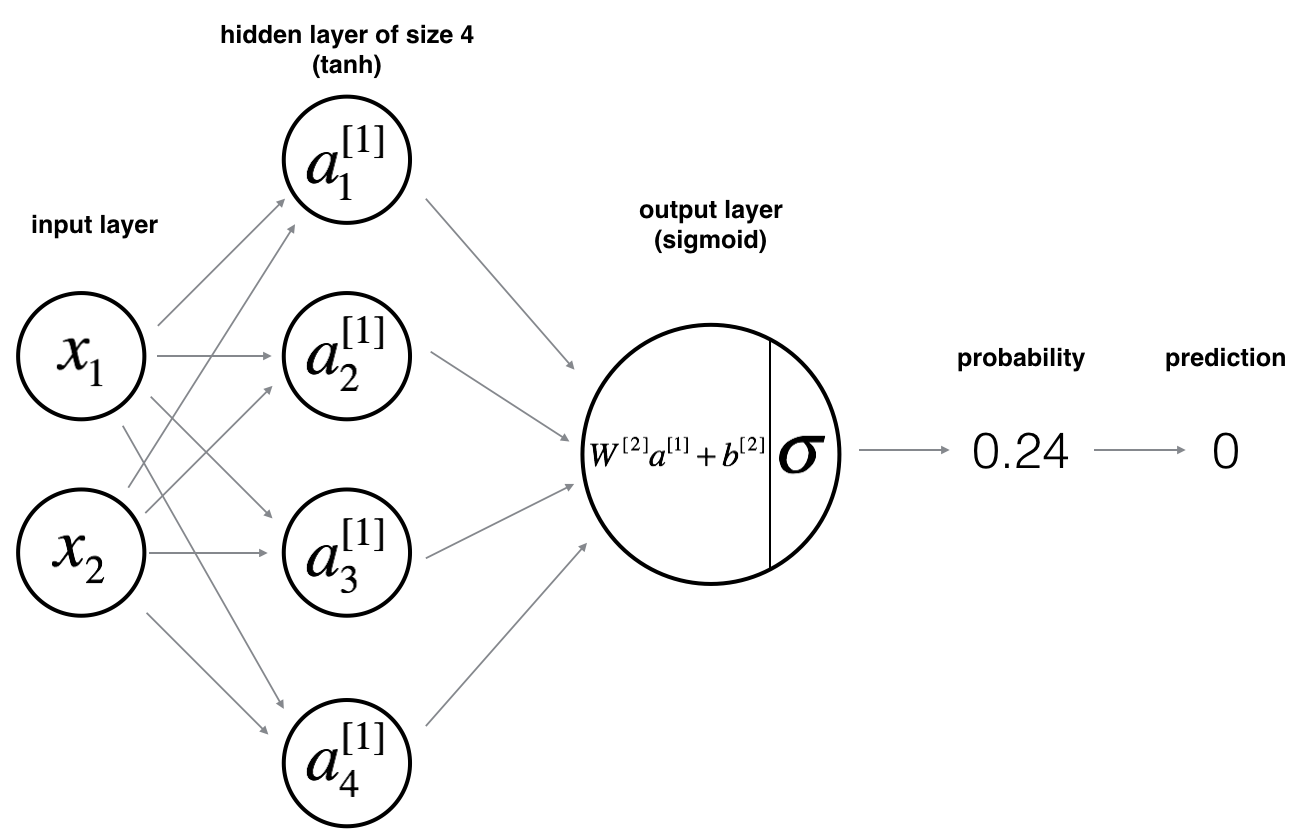
Reminder: The general methodology to build a Neural Network is to: 1. Define the neural network structure ( # of input units, # of hidden units, etc). 2. Initialize the model's parameters 3. Loop: - Implement forward propagation - Compute loss - Implement backward propagation to get the gradients - Update parameters (gradient descent)
初始化参数
先定义模型的每一层大小,输入层通过输入的数据数量判断,输出层通过标签数据判断,隐藏层硬编码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22# GRADED FUNCTION: layer_sizes
def layer_sizes(X, Y):
"""
Arguments:
X -- input dataset of shape (input size, number of examples)
Y -- labels of shape (output size, number of examples)
Returns:
n_x -- the size of the input layer
n_h -- the size of the hidden layer
n_y -- the size of the output layer
"""
#(≈ 3 lines of code)
n_x = X.shape[0]
n_h = 4
n_y = Y.shape[0]
# YOUR CODE STARTS HERE
# YOUR CODE ENDS HERE
return (n_x, n_h, n_y)然后初始化w和b数组,这里需要注意对于w需要使用randn函数,因为这样可以生成遵循标准正态分布的随机数,即都在0周围。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32# GRADED FUNCTION: initialize_parameters
def initialize_parameters(n_x, n_h, n_y):
"""
Argument:
n_x -- size of the input layer
n_h -- size of the hidden layer
n_y -- size of the output layer
Returns:
params -- python dictionary containing your parameters:
W1 -- weight matrix of shape (n_h, n_x)
b1 -- bias vector of shape (n_h, 1)
W2 -- weight matrix of shape (n_y, n_h)
b2 -- bias vector of shape (n_y, 1)
"""
#(≈ 4 lines of code)
W1 = np.random.randn(n_h,n_x)*0.01
b1 = np.zeros((n_h,1))
W2 = np.random.randn(n_y,n_h)*0.01
b2 = np.zeros((n_y,1))
# YOUR CODE STARTS HERE
# YOUR CODE ENDS HERE
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
有了w和b我们部署循环,即
- 进行正向传播
- 计算损失函数
- 反向传播获取梯度
- 使用梯度进行梯度下降更新w和b
正向传播:
使用如下等式:均为矩阵点乘
\[Z^{[1]} = W^{[1]} X + b^{[1]}\tag{1}\] \[A^{[1]} = \tanh(Z^{[1]})\tag{2}\] \[Z^{[2]} = W^{[2]} A^{[1]} + b^{[2]}\tag{3}\] \[\hat{Y} = A^{[2]} = \sigma(Z^{[2]})\tag{4}\]
1 | # GRADED FUNCTION:forward_propagation |
计算损失函数:
对于预测值数组A2使用如下等式:
\[J = - \frac{1}{m} \sum\limits_{i = 1}^{m} \large{(} \small y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \large{)} \small\tag{13}\]
1 | # GRADED FUNCTION: compute_cost |
部署反向传播:
在向量化实现中使用右侧的六个等式来计算。g1在这里是tanh激活函数,导数是1-g2,所以这里就是1-A12
1 | # GRADED FUNCTION: backward_propagation |
更新参数
General gradient descent rule: \(\theta = \theta - \alpha \frac{\partial J }{ \partial \theta }\) where \(\alpha\) is the learning rate and \(\theta\) represents a parameter.
注意记得乘学习率
1 | # GRADED FUNCTION: update_parameters |
组合代码
使用上述代码实现model()函数
1 | # GRADED FUNCTION: nn_model |
使用模型进行预测
1 | # GRADED FUNCTION: predict |
Deep Neural Network
层数=hidden+ output,用L来表示。用\(n^{[L]}\)表示第L层单元的数量。
N1 = 第一个隐藏层
使用for循环计算每一层的正向传播。
神经网络中矩阵形状
对每一层参数矩阵,有
\(W^{[L]}:(n^{[L]},n^{[L-1]})\)
\(b^{[L]}:(n^{[L]},1)\)
\(dW^{[L]}:(n^{[L]},n^{[L-1]})\)
\(db^{[L]}:(n^{[L]},1)\)
输入有m个的时候,X矩阵是\((n^{[0]},m)\)大小的
因此:
\(Z^{[1]}:(n^{[1]},m)\)
\(dZ^{[1]}:(n^{[1]},m)\)
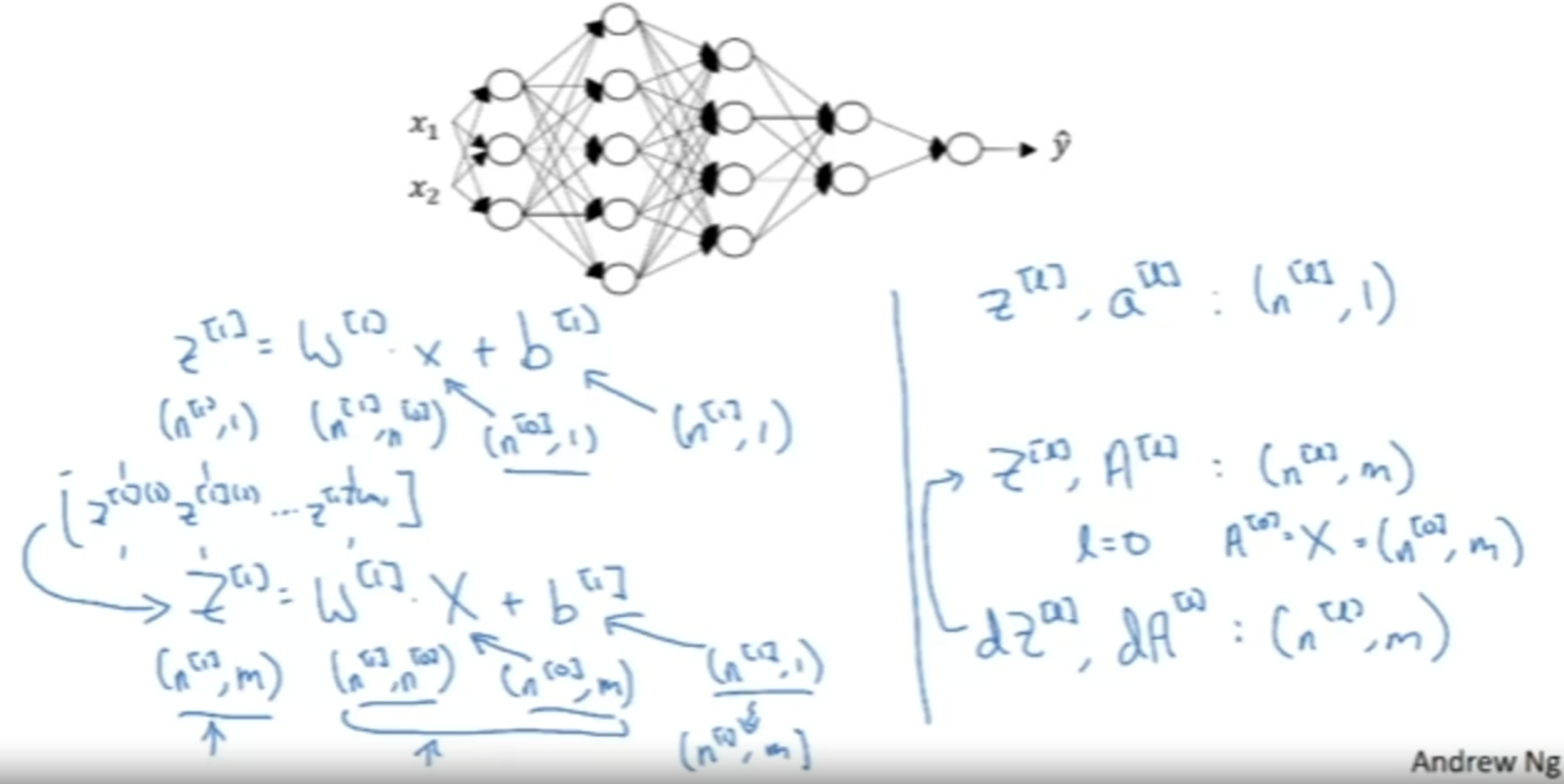
为什么深度网络效率高?
在深度网络中,每一层可以从细微到宏观地识别各种特征。
如第一层可以用来检测边缘,下一层检测更多特征。
深度神经网络中的正向和反向传播
理论基础
General forward propagation:
Input \(a^{[l-1]}\),output \(a^{[l]}\)
By the equation: \[ Z^{[l]} = \omega^{[l]}a^{[l-1]}+b^{[l]} \]
\[ a^{[l]} = g^{[l]}(Z^{[l]}) \]
这时可以cache一个Z(l)在一会的反向传播使用。
General backward propagation:
Input \(da^{[l]}\),output \(da^{[l-1]}\)
这时会用到刚刚的Z(l),然后使用输出的da来更新dw和db。
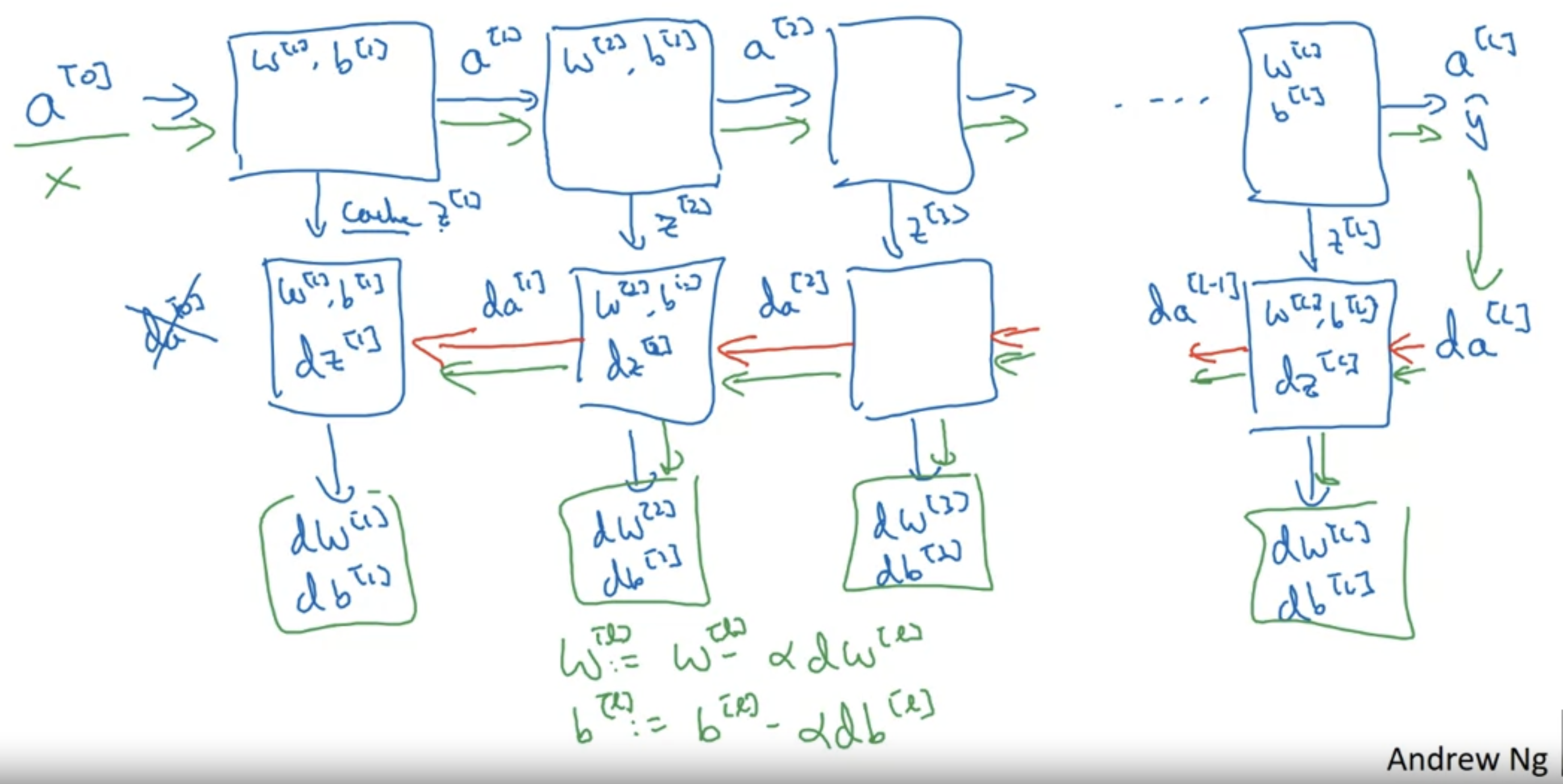
具体实现:
正向传播使用这个公式计算
\[ Z^{[l]} = \omega^{[l]}A^{[l-1]}+b^{[l]} \]
\[ A^{[l]} = g^{[l]}(Z^{[l]}) \]
反向传播: \[ dZ^{[l]} = dA^{[l]}*g^{'[l]}(Z^{[l]}) \]
\[ d\omega^{[l]} = \frac{1}{m}dZ^{[l]}A^{[l-1]T} \]
\[ db^{[l]} = \frac{1}{m}np.sum(dZ^{[l]},axis=1,keepdims=True) \]
\[ dA^{[l-1]} = \omega^{[l]T}dZ^{[l]} \]
Parameters v. Hyperparameters
Parameters: W,b
Hyperparameters: learning rate, iterations, hiddenlayers....
Improving Deep Neural Networks
Practical Aspects of Deep Learning
Setting up Machine Learning Application
对手里的数据进行划分,一部分训练一部分测试。
如果数据集很小的话可以用60/20/20的比例分割训练,开发,测试集
如果数据集很大的话只需要一点来做测试和开发就可以。
Bias/Variance
Bias高会导致欠拟合,Var高会导致过拟合,具体表现为:如果训练集误差很低,测试集误差很高,那就是过拟合。如果都高且差的不多就是欠拟合。
Bayes Error: 在分类问题中,针对某个样本的最小误差。这个误差与数据本身的不确定性有关,他代表理论上无法超越的分类性能下限,无论用什么分类器都不能把误差降到贝叶斯误差以下。
bias大可以通过更大的模型/更久的训练时间来解决
var大可以通过更多数据/正则化regularization解决
Regularization正则化
用于解决过拟合问题
在逻辑回归模型中,正则化有以下公式: \[ J(w,b)=\frac{1}{m} \sum_{i=1}^{m} L(\hat{y}^{(i)}, y^{(i)})+\frac{\lambda}{2m} \|\omega^{[l]}\|_2^2 \] 后边这一项叫做\(L_2\)范数,他是模型中所有权重的平方和。
在深度神经网络中,通过添加lambda参数来实现:
- 损失函数 (J):
\[ J(\omega^{[1]}, b^{[1]}, \ldots, \omega^{[L]}, b^{[L]}) = \frac{1}{m} \sum_{i=1}^{m} L(\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2m} \sum_{l=1}^{L} \|\omega^{[l]}\|_2^2 \]
Frobenius 范数 :
他是网络中所有w的平方和。
\[ \|\omega^{[l]}\|_F^2 = \sum_{i=1}^{n^{[l+1]}} \sum_{j=1}^{n^{[l]}} (\omega_{ij}^{[l]})^2 \]
- 权重矩阵的维度 :
\[ \omega^{[l]} : (n^{[l+1]}, n^{[l]}) \]
Dropout Redularization
在训练过程中随机“丢弃”一部分神经元来提高模型的泛化能力。
具体实现时,以固定概率p来随机丢弃神经元,被丢弃的神经元在这一次迭代中不会参与正向和反向传播。每次迭代中丢弃的神经元是随机选择的,这样模型就不会依赖某些特定的神经元。常用的p是0.2-0.5之间,丢弃只会在训练过程中使用。
Data augmentation
对旧数据进行修改来训练可以获得更多训练集来解决过拟合问题。
图片中可以进行如翻转或裁剪。
Early stopping
在训练过程中监控模型在验证集上的性能,当性能不在改善的时候就停止训练来防止模型过拟合。
归一化输入数据
用来加快训练速度 \[ x_{norm}=\frac{x - \mu}{\sigma} \]
假如输入X是一些坐标(x1,x2),可以对所有输入减去他们的平均值\(\mu = \frac{1}{m}\sum_{i=1}^mx^\)可以让数据都到中心位置。
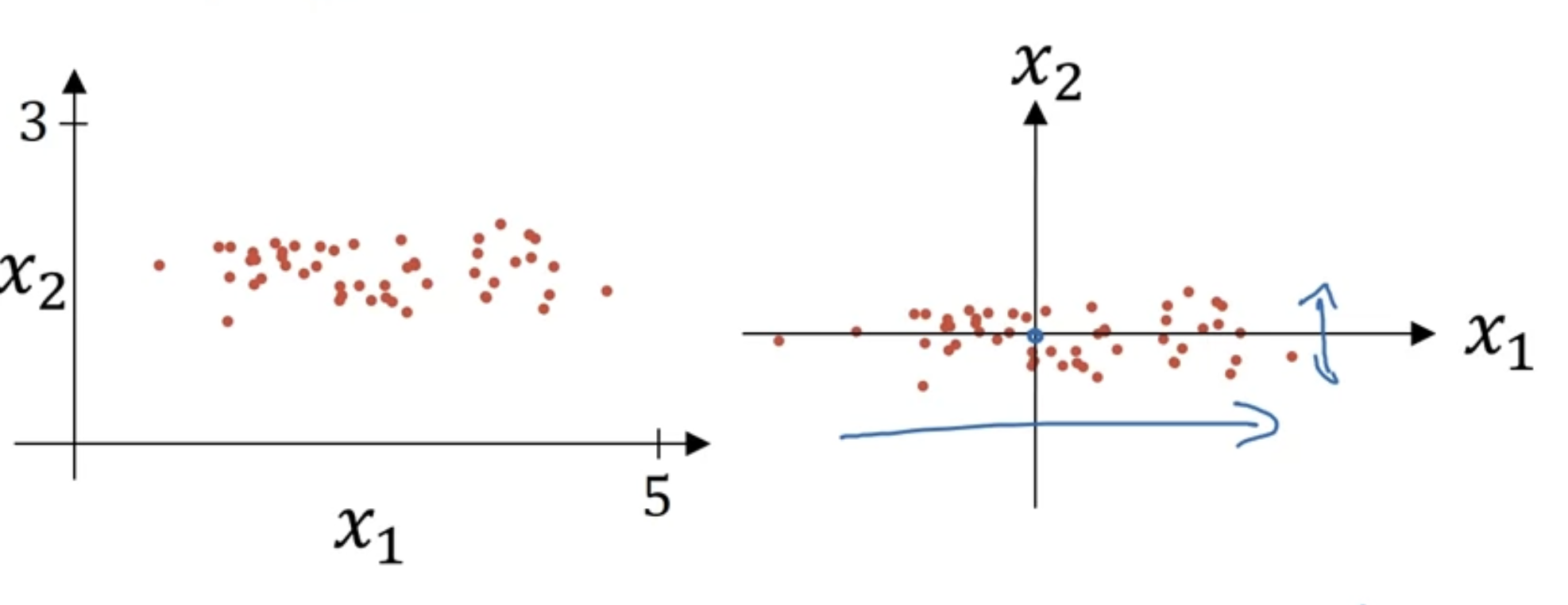
这时发现x1的方差比x2大,我们还需要再归一化方差:
\(\sigma^2 = \frac{1}{N}\sum^N_{i=1}(x_i-\mu)^2\)
开平方后得到标准差。
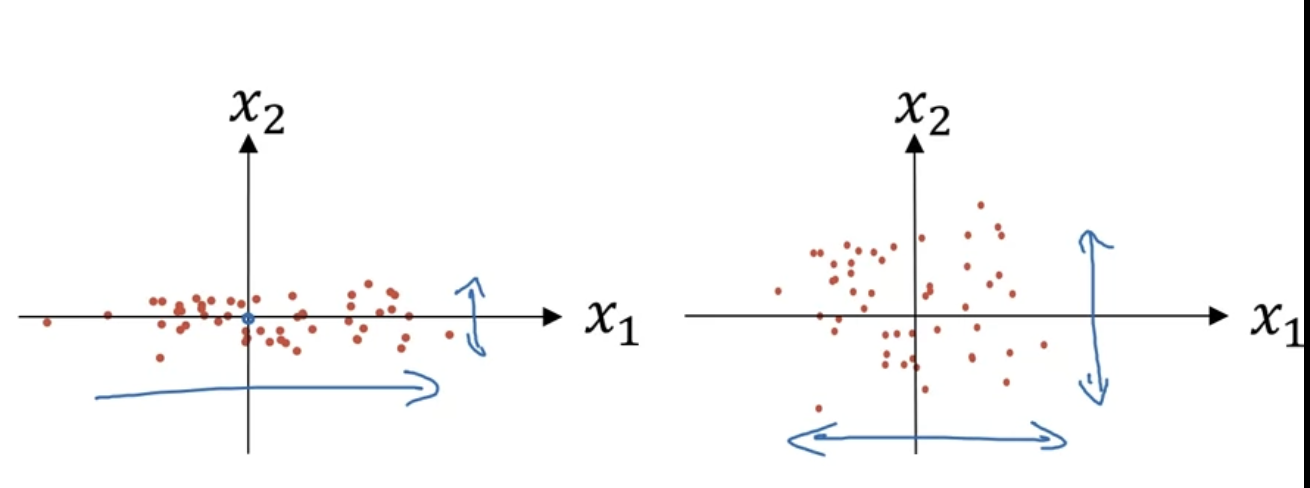
如果数据比例不一样,如有的是0-1,有的是0-1000就可以进行归一化,不过做了归一化也没什么坏处。
梯度消失/梯度爆炸
Gradient checking
Optimization Algorithms
Mini-batch gradient descent
把输入的X,Y矩阵分成很多个小矩阵。
假设X是(n,m)大小,n是input size,即样本的特征数量。m是样本的数量(number of examples).Y是(a,m)大小,a是output size,即输出类型,m是样本数量,即对每一个样本都有一个输出。
mini-batch的时候把m个样本分成很多份,然后用for循环对每个batch进行训练。每个batch的一轮处理叫做一个epoc。
mini-batch训练时的cost下降会有一些波动,因为具体效果取决于每个batch里数据,有可能有数据有噪音导致学习效果不好。
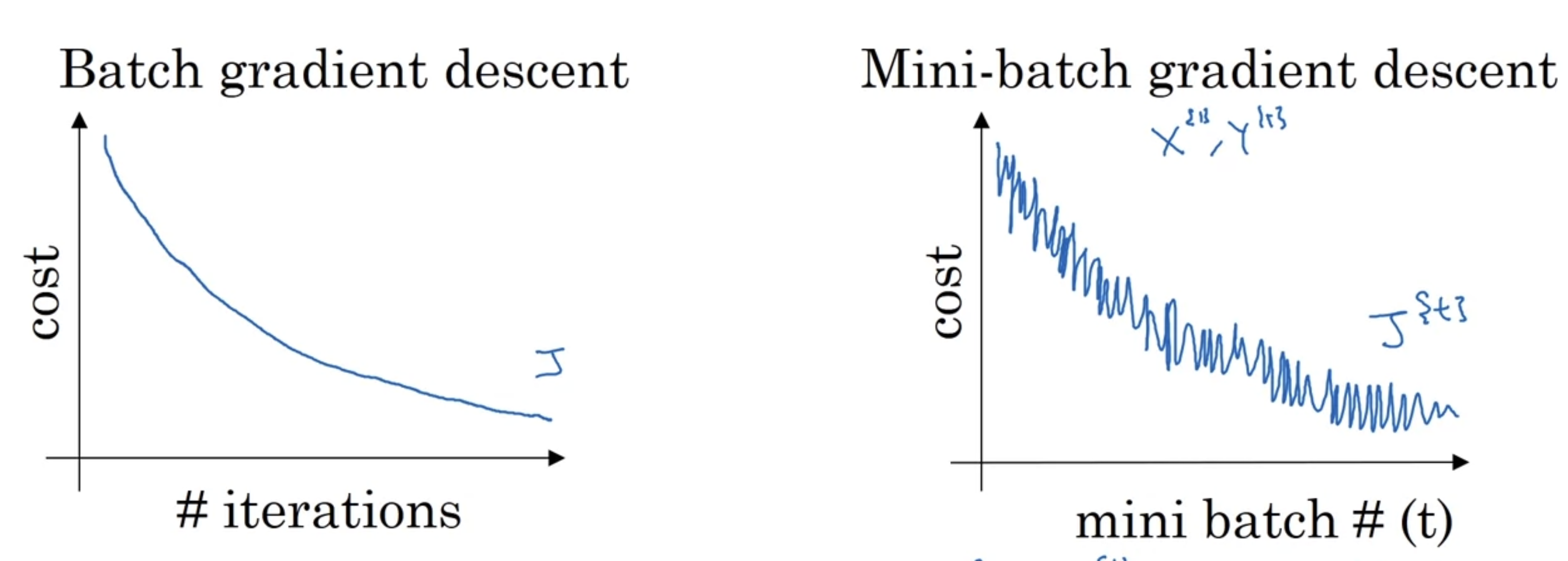
在使用mini-batch的时候需要指定它的参数:每个batch里的数据大小。大小可以指定为64-1024之间的某个值
Exponentially weighted average指数加权平均数
用来处理时间序列数据,他赋予最近的观测值最大的权重,最早的观测值最小的权重。 \[ v_t = \beta v_{t-1} + (1 - \beta) x_t \]
- \(\beta\)是平滑因子,范围0-1
- vt是在t时间的数据的加权平均数
- xt是时间t处的观测值
可以用来计算一段时间的平均数据,如一个月内每天的平均气温。
但是用这个平均数直接计算会在一开始的时候有误差,这时就要使用误差修正(bias correction):
使用\(\frac{v_t}{1-\beta^t}\)来代替原来的vt可以修正这个问题。t很小的时候可以有更准确的数据,t变大的时候这个值和原来的vt几乎一样。
Gradient Descent with momentum
- 在每次迭代的时候,在每个mini-batch里计算dw和db
- 计算\(vd_w = \beta V_{dw} + (1-\beta)d_w\)
- \(V_{db} = \beta V_{db}+ (1-\beta)d_b\)
- \(W = W-\alpha V_{dw}, b = b - \alpha v_{db}\)
一般设置\(\beta\)为0.9
RMSprop
与momentum差不多,只不过\(S_{db}=\beta S_{db} + (1-\beta)d_b^2\)
然后 \(w = w - \alpha \frac{dw}{\sqrt{S_{dw}+\epsilon}}\)
Adam Optimization Algorithm
组合RMS和momentum
首先,初始化Vdb,Vdw,Sdb,Sdb都为0
然后在每次迭代中
- 计算\(vd_w = \beta V_{dw} + (1-\beta)d_w\), \(V_{db} = \beta V_{db}+ (1-\beta)d_b\)
- 计算\(S_{db}=\beta S_{db} + (1-\beta)d_b^2\),
注意这里两个beta不是一个。
- 应用bias correction , \(V_dw = \frac{V_dw}{1-\beta^t}\),对四个参数都应用correction
- 更新w和b:\(w = w - \alpha \frac{V_dw}{\sqrt{S_{dw}+\epsilon}}\)
一般beta1(Vdw的参数)设置为0.9,beta2\((Sdw^2)\)设置为0.999,\(\epsilon\)设置为10^-8,这些也是Adam的默认参数。使用这些默认参数后调试学习率alpha来训练。
Learning Rate Decay
在训练过程中可以逐渐减小学习率,因为后期不需要步长很长。
可以使用以下几种方法:
\(\alpha = 0.95^{epochnum} *\alpha_0\)
\(\alpha = \frac{k}{\sqrt{epochnum}}*\alpha_0\)
或者手动调整学习率。
Hyperparameter Tuning
Batch Normalization 批量归一化
在之前讨论过归一化normalization问题,先减均值再除平均差。
现在需要对中间变量进行归一化。对Z(i)进行归一化处理。
例如:输入X后经过第一层得到Z[1],然后对Z1进行归一化后经过激活函数得到a1,然后用这个a1再进入下一层,以此类推。
Softmax multi-class classification Regression
输出可以有多个值,最后一层使用softmax层实现,也就是对上一层结果Z运用softmax激活函数。
具体来说,首先计算一个\(t=e^{z[L]}\), 然后\(a = \frac{t}{\sum^4_{j=1}t_i}\).,其实就是算出每个结果对应的t之后求出他在所有求和之中站的比例,然后这个比例就是他是这个的概率。
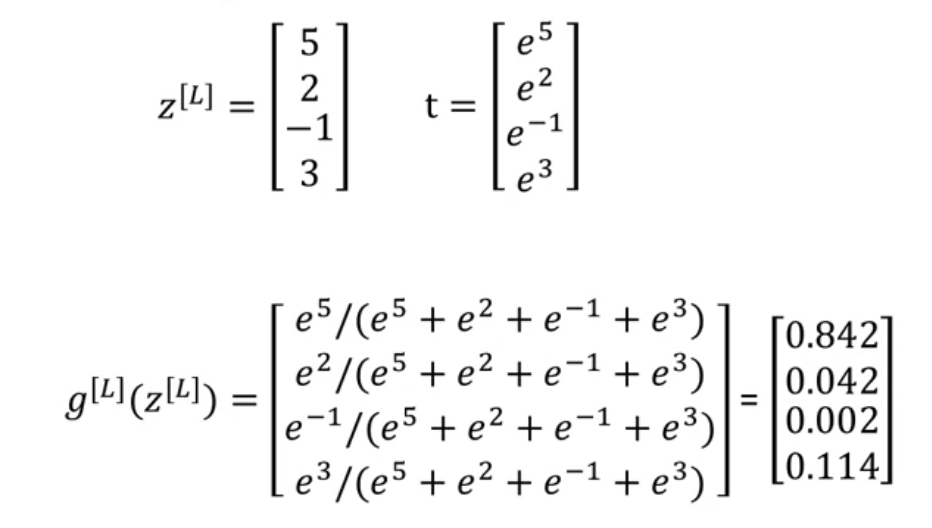
Intro to Tensorflow
假设目前需要最小化cost function \(J = (x-5)^2\)
用w = tf.Variable(0,dtype=tf.float32)来定义tf中的变量,即神经网络里的w。

核心是定义cost function,